Last update 17.04.2000
Copyright Frank Maraite 2000
GeoCAD-R
E.2.2
 Standard
Stichworte Zweck, Vorausetzung, Ablauf, Aufruf, Menüpunkte
Zweck Das Untermenü "Standard" enthält die in der Katastervermessung meistbenutzen Berechnungsarten.
Voraussetzung Sie müssen ein Projekt (Auftrag) angelegt und aktivieren (siehe Kap. E.1.1.1 bzw. Kap. E.1.1.2), um alle Menüpunkte zuzugänglich zu machen.
Ablauf Sie rufen im Hauptmenü den Menüpunkt "Standard" auf.
Aufruf 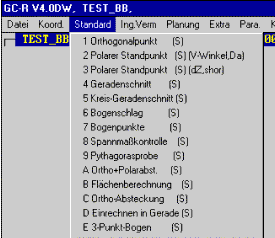Aufruf: Standard (5 KB)
Menüpunkte Erläuterung der Menüpunkte.
Orthogonalpunkt Die Berechnungen von ebenen oder räumlichen Koordinaten nach der Methode der Orthogonalaufnahme (siehe Kap. E.2.2.1). Zudem enthält der Menüpunkt eine Pythagorasprobe.
Polarer Standpunkt
(V-Winkel, DA)		 Bestimmung von ebenen oder räumlichen Koordinaten nach der Methode der Polaraufnahme (siehe Kap. E.2.2.2). Diese Variante arbeitet mit der Zenitdistanz und der Schrägentfernung.

Sie ist Voraussetzung für die Berechnung eines ebenen oder räumlichen "Polygonzuges", eines ebenen oder räumlichen "Vorwärtsschnittes", "Vertikalschnittes" oder einer ebenen oder räumlichen "Freien Stationierung".
Polarer Standpunkt
(dZ, shor)		 Bestimmung von ebenen oder räumlichen Koordinaten nach der Methode der Polaraufnahme (siehe Kap. E.2.2.3).

Dieser Ansatz wird fast ausschließlich durch einen Ansatz Satzmessung (siehe Kap. E.2.3.5) automatisch erstellt. Der Unterschied zum Ansatz "Polarer Standpunkt (V-Winkel, DA)" ist, daß hier mit dem Höhenunterschied und der Horizontalentfernung gearbeitet wird.

Sie ist Voraussetzung für die Berechnung eines ebenen oder räumlichen "Polygonzuges", eines ebenen oder räumlichen "Vorwärtsschnittes", "Vertikalschnittes" oder einer ebenen oder räumlichen "Freien Stationierung".
Geradenschnitt Bestimmung von ebenen oder räumlichen Koordinaten durch die Methoden des Geraden-, Lot- und Parallelschnittes (siehe Kap. E.2.2.4).
Kreis-Geradenschnitt Bestimmung des Schnittpunktes eines Kreises mit einer Geraden (siehe Kap. E.2.2.5).
Bogenschlag Bestimmung eines oder mehrerer Punkte durch Bogenschlag von zwei gegebenen Punkten aus (Schnitt zweier Kreise). Bestimmung der orthogonalen Absteckwerte der Neupunkte bezogen auf die beiden gegebenen Punkte (Höhe und Höhenfußpunkt) (siehe Kap. E.2.2.6).
Bogenpunkte Berechnen von Punkten auf einem Kreisbogen und dazu parallelen Kreisbögen. Dem Bogenanfang kann eine von Null verschiedene Station zugeordnet werden. Falls auch ein Bogenendpunkt eingegeben wird, kann durch Variation der Zahl der Zwischenpunkte eine optimale Pfeilhöhe ermittelt werden (siehe Kap. E.2.2.7).
Spannmaßkontrolle Mit diesem Programm können ebene Kontroll- oder Spannmaße geprüft werden (siehe Kap. E.2.2.8).

Räumliche Spannmaßkontrollen finden Sie im Kapitel E.2.5.C. 
Pythagorasprobe Rechnet in örtlichen, rechtwinkligen Dreiecken die Streckenkontrolle (siehe Kap. E.2.2.9).
Ortho+Polarabst. Bestimmung der Absteckwerte von bereits vorliegenden Punkte (Koordinaten) bezüglich einer Standlinie, definiert durch Anfangs- und Endpunkt. Dabei werden sowohl orthogonale (Abszisse u. Ordinate) wie polare (Richtung u. Strecke) Absteckwerte berechnet.

Diese werden sowohl auf den Anfangs- (PA) wie auch auf den Endpunkt (PE) bezogen (siehe Kap. E.2.2.A).
Flächenberechnung Mit dem Programm Flächenberechnung werden Flächeninhalte von Polygonen, auch durch Bögen begrenzte, bestimmt (siehe Kap. E.2.2.B). Zudem werden bei dreieckigen Flächen Volumeninhalte berechnet (Prismenmethode).

Neben der Fläche rein aus Koordinaten werden wahlweise auch die Fläche in der Gauß-Krüger-Ebene und/oder in der Geländehöhe ausgegeben.
Ortho-Absteckung Projekt als Katasterauftrag a) oder als Ingenieurauftrag b):
  • a) Vergleich zwischen örtlich bestimmten und aus Koordinaten berechneten Messungslinien (siehe Kap. E.2.2.C).
  • b) Ausgabe der Signatur und deren Bezeichnung (siehe Kap. E.2.2.C). Wahlweise ist die Ausgabe in eine CADDY-Längsschnittdatei möglich.
Einrechnen in Gerade Bestimmt Punkte (Koordinaten), die z.B. polar aufgemessen wurden, um dann zwangsweise in eine Gerade eingerechnet werden sollen (siehe Kap. E.2.2.D).

Das bisherige Ordinatenmaß wird mit ausgegeben.
3-Punkt-Bogen Berechnet aus drei Punkten den Kreismittelpunkt, Radius, Umfang, Stationierung und Bogenlänge. Dazu Schnittwinkel und Zentriwinkel (siehe Kap. E.2.2.E).